Mějme dáno n + 1 opěrných bodů P0, P1, ..., Pn. Splajn křivkou m-tého řádu rozumíme funkci f(z), která má spojité derivace f0, f'(z), ..., f(m-1) a na každém intervalu <xi, xi+1> je f(x) polynomem stupně m. Splajn křivka se tedy skládá z polynomů a zaručuje spojitost derivací v navazovacích bodech.
Splajn křivky jsou jistým zobecněním polynomiálních interpolací a aproximací. Teorie splajn křivek je velice obsáhlá a patří spíše do matematiky než do počítačové grafiky. Svůj přínos v CAGD mají teorie g -splajn a ß-splajn, které se zabývají zobecněním tzv. geometrické spojitosti. Podrobnějsí informace je možno nalézt v [Drdl92], [Drs84], [Drs85] a [Drs90].
Uniformní neracionální kubický B-splajn se také nazývá kubický Coonsův B-splajn.
Vznikne navázáním Coonsových kubik ( 7.2 ) takto :
segment Qi je určen body Pi-3, Pi-2,
Pi-1 a Pi. Následující segment Qi+1
je složen z bodů Pi-2, Pi-1, Pi
a Pi+1, tedy ze tří posledních bodů segmentu Qi
a z jednoho bodu nového atd. Coonsův B-splajn je určen n + 1 body.
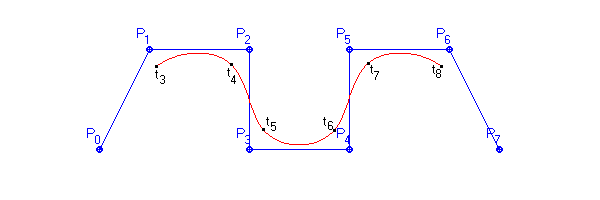
Obr. 10.1: Coonsův kubický B-splajn
Applet. 10.1 Coonsův kubický B-splajn
Porovnáme-li vztahy pro tečné vektory a vektory druhých derivací dvou po sobě následujících segmentů Qi a Qi+1, zjistíme, že segment Qi+1 vychází z posledního bodu segmentu Qi a že jsou identické první a druhé derivace v tomto bodě. Křivka je tedy v uzlech C2 spojitá.
Využijeme-li chování Coonsových kubik při násobnosti bodů, tak posloupností P0, P0, P0, ... P1, ..., Pn-l, Pn, Pn, Pn zajistíme, že výsledný kubický splajn bude procházet krajní body svého řídicího polygonu, ovšem za tu cenu, že první segment bude úsečkou spojující bod P0 s bodem ležícím na jedné šestině vzdálenosti P0Pl a analogicky na konci řídicího polygonu.
 |
|
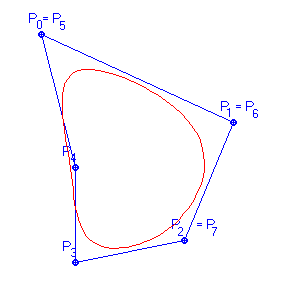
Obr. 10.2 Uzavřený B-splajn |
Applet 10.2 Uzavřený B-splajn |
Uzavřený B-splajn (Obr. 10.2) získáme opakováním n prvních bodů řídicího polygonu na jeho konci. Pro kubický B-splajn je tedy řídícím polygonem uzavřené křivky posloupnost bodů: P0, Pl, ..., Pm, P0, Pl, P2.
Coonsův kubický B-splajn generovaný n+1 body řídicího polygonu P0, P1, ..., Pn, je složen z n - 2 segmentů Q3, Q4, ..., Qn (Obr. 10.1). Parametr t probíhá interval <0, n+1> a hodnoty parametru t v uzlech (označujeme je ti) definují uzlový vektor (angl. knot vector).
Tyto hodnoty mají konstantní vzdálenost ti+1 - ti = k, uzlový vektor je uniformní (odtud i název těchto křivek).
Mezi důležité vlastnosti B-splajn křivek patří invariance vůči rotaci, translaci a změně měřítka, B-splajn křivka leží celá ve své konvexní obálce a její segmenty leží v konvexních obálkách svých řídicích polygonů. Zvláště poslední vlastnost nám umožní pochopit následující text :
Lokalita změny znamená, že pokud posuneme některý z řídících bodů, změní se tvar pouze v té části Coonsova B-splajnu, který je tímto bodem generován. Pokud posuneme bod Pi kubiky Q(t), změní se tvar čtyř segmentů Qi, Qi+1, Qi+2 a Qi+3. Na obrázku (Obr. 10.3) jsou dvě křivky. První je určena řídicím polygonem P0, P1, ..., P8. Druhá se od první liší pouze tím, že bod P4 je posunut do polohy P4. Uzly jsou označeny t3 až t9. Je patrné, že změnou polohy jediného bodu se změnila také poloha uzlů t5 až t7. Vždy dva uzly určují hranice segmentu, došlo tedy ke změně tvaru čtyř segmentů.
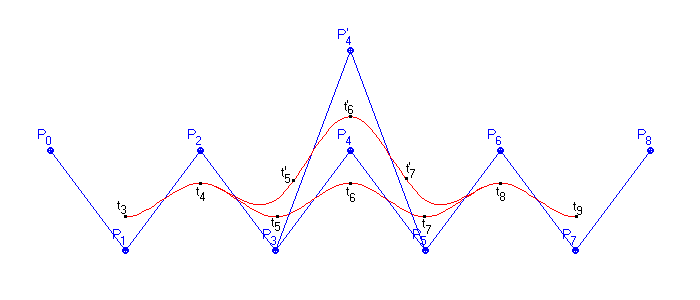
Obr.10.3 Lokalita změny tvaru křivky při změně polohy bodu řídícího polygonu. Uzlové vektory jsou označeny body t3 až t9.
Applet 10.3 Lokalita změny tvaru křivky při změně polohy bodu řídícího polygonu. Uzlové vektory jsou označeny prázdnými kolečky.
Díky tomu, že segment leží v konvexní obálce svého řídicího polygonu, je možné snadno pochopit co se stane, je-li některý bod řídicího polygonu vícenásobný. Podívejme se na obrázek (Obr. 10.1) a sledujme, co se bude dít, budeme-li zvyšovat násobnost bodu P3. Segment Q4 je určen uzly t4 a t5 a řídicím polygonem P1, P2, P3, P4 a segment Q5 uzly t5 a t6 a řídicím polygonem P2, P3, P4, P5. V případě, kdy není žádný bod několikanásobný, jsou všechny řídicí polygony čtyřúhelníky a konvexní obálky dvou po sobě následujících segmentů, pro náš případ řídicí polygony segmentů Q4 a Q5 mají společnou plochu vymezenou trojúhelníkem P2, P3, P4. V této oblasti také leží společný uzel t5. Na obrázku (Obr. 10.4) zdegenerovaly čtyřúhelníky P1, P2, P3, P4 a
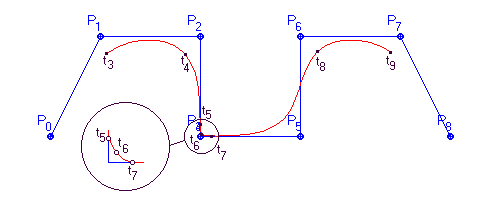
Obr. 10.4 Dvojnásobný bod
Applet 10.4 Dvojnásobný bod
P2, P3, P4, P5 na trojúhelníky tím, že překrývající se oblastí je společná hrana P2P3. Na této hraně musí leží uzel t5.
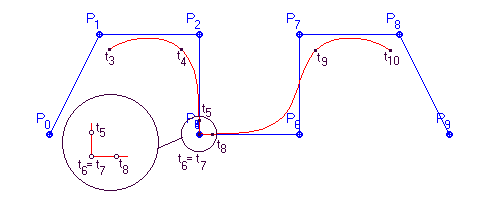
Obr. 10.5 Trojnásobný bod
Applet 10.5 Trojnásobný bod
Na obrázku (Obr. 10.5) je bod P3 trojnásobným bodem, konvexní obálka P2 až P5 degeneruje na úsečku P2P3, stejně jako segment Q5 degeneruje na úsečku ležící na P2P3.
Applet pro experimenty :