S. A. Coons definoval metodu, která má své silné použití díky dobrým geometrickým vlastnostem hlavně v navrhování ploch. Její princip je však vhodné vyložit na modelování křivek.
Coonsova kubika se zadává stejně jako kubika Bézierova čtyřmi řídicími body P0, Pl, P2, a P3. Coonsova kubika se spočítá ze vztahu :
![]()
kde C0, C1, C2, C3 jsou kubické polynomy tvaru:
C0(t) = (1 - t)3,
C1(t) = 3t3 - 6t2 + 4,
C2(t) = -3t3 + 3t2 + 3t
+ 1,
C3(t) = t3
t Î < 0,1 >.
Maticově zapsáno:
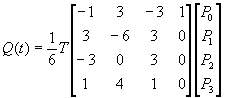
( 9.3 )
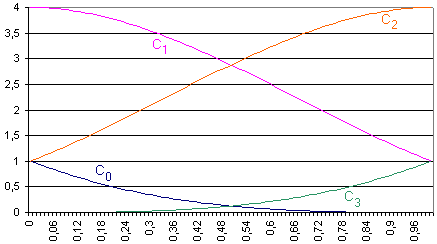
Obr. 9.1 Kubické polynomy Coonsovy kubiky
Ze vztahů ( 9.1 ) a ( 9.2 ) plyne, že po dosazení t = 0 je:
![]()
( 9.4 )
pro t =1 je:
![]()
( 9.5 )
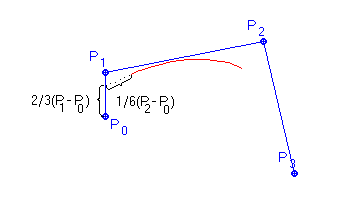
krajní body křivky tedy nevychází z řídicích bodů, ale z antitěžiště trojúhelníků P0PlP2 a P1P2P3 (Obr. 9.2).
 |
|
Obr. 9.2 Coonsova kubika |
Applet 9.2. Coonsova kubika |
Derivací vztahu ( 9.1 ) dostaneme
![]()
( 9.6 )
Pro t = 0 je C'0(0) = -3, C'1(0) = 0, C'2(0) = 3, C'3(0) = 0. Odtud plyne, že
![]()
( 9.7 )
![]()
Největší výhoda Coonsových kubik se stane zřejmou teprve v okamžiku, kdy je použijeme pro skládání aproximačních křivek. Uvažujme řídicí polygon složený z bodů P0, P1, ..., Pn. Budeme-li výslednou křivku skládat z Coonsových oblouků vždy tak, že pro jeden oblouk použijeme vrcholy P0P1P2P3, pro další P1P2P3P4 atd., získáme křivku, která se nazývá B-splajn.
Vlastností B-splajnu je, že má ve všech vnitřních bodech spojitost druhého řádu. Z hlediska konstrukce je pro tímto způsobem vytvářenou křivku výhodné i to, že změnou jednoho bodu dojde pouze k lokální změně čtyř oblouků, jejichž konstrukce se bod účastní.
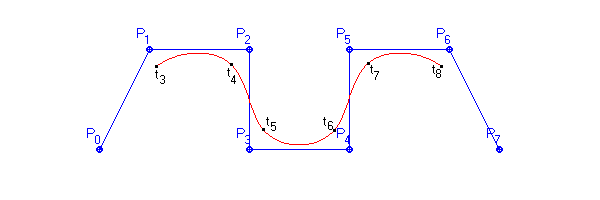
Obr. 9.2 Coonsův kubický B-splajn
Applet. 9.2 Coonsův kubický B-splajn
Applet pro experimenty: