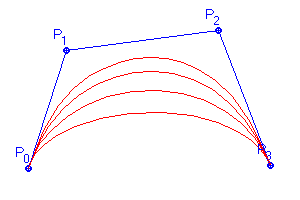
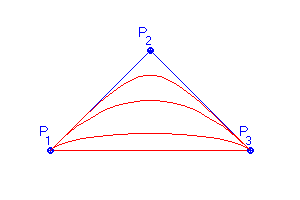
Poměrně novou metodou v CAGD je teorie racionálních Bézierových křivek. Jak napovídá název, jedná se o zobecnění Bézierových křivek. Při klasickém zadávání Bézierových křivek zadává uživatel řídicí polygon a program podle jeho požadavků buď proloží body křivkou patřičného řádu, nebo výslednou křivku složí z křivek řádu nižšího. Pokud chce uživatel změnit tvar křivky, musí identifikovat bod a změnit jeho polohu. To nemusí být vždy výhodné. Pokud se pracuje v rovině, neprojeví se tento problém tak, jako v trojrozměrném prostoru. Identifikace bodu v prostoru však není vůbec triviální a hlavně nebývá nijak názorná. Přirozenou se potom jeví metoda, která každému bodu řídicího polygonu přiřadí reálné číslo, jehož změnou se mění tvar křivky (Obr. 8.1).
 |
|
Obr. 8.1 Změna tvaru křivky s koeficienty v bodech P1 a P2 postupně 0.25, 0.5, 1 a 5 |
Applet 8.1 Změna tvaru křivky s koeficienty v bodech P1 a P2 |
Racionální Bézierova křivka je určena posloupností bodů P0, P1, ..., Pn, a posloupností reálných čísel w 0, w l, ..., w n. Bézierova racionální křivka řádu n je potom určena vztahem:
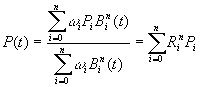
( 8.1 )
V tomto vztahu je i = 0, l, ..., n Î N, w >= 0 reálné číslo a
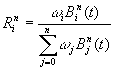
![]() jsou Bernsteinovy polynomy ( 4.2
) a
jsou Bernsteinovy polynomy ( 4.2
) a ![]() ( 8.2 ) jsou racionální
Bernsteinovy polynomy.
( 8.2 ) jsou racionální
Bernsteinovy polynomy.
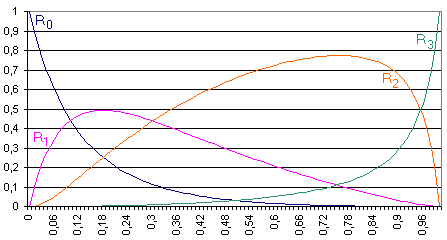
Obr. 8.2 Racionální Bersteinovy polynomy pro (w0, . . ., w3) = (1, 3, 7, 1)
Podobně jako u Bernsteinových polynomů lze i u racionálních Bernsteinových polynomů dokázat, že :
Poslední vztah lze snadno dokázat ze vztahu druhého. Vyplývá z něho, že racionální Bézierovy křivky jsou opravdu zobecněním Bézierových křivek (Bézierovy křivky jsou zvláštním případem racionálních, kde jsou koeficienty wi rovny jedné pro všechna i). Pro racionální Bézierovy křivky platí:
P(0) = P0, P(1) = Pn.
Dosazením lze dokázat, že křivka prochází počátečním a koncovým bodem řídicího polygonu.
![]() ,
, ![]()
( 8.3 )
Vztahy pro tečny v krajních bodech. Dosadíme-li za w i jedničku, obdržíme výše uvedené vztahy pro tečny obecných Bézierových křivek. Bude-li w i >= 0, i = 0, 1, ... , n, leží výsledná aproximační křivka v konvexní obálce bodů řídicího polygonu. Zvýšení stupně aproximační křivky P0, P1, ..., Pn, w 0, w 1, ..., w n bez změny jejího tvaru docílíme přidáním libovolného bodu tak, že vznikne nová a Q0, Q1, ..., Qn+1, w 0, w 1, ..., w n+1. Pro nové body platí:
![]() ,
,
( 8.4 )
v tomto vztahu je
![]() ,
,
![]() .
.
( 8.5 )
Jak bylo uvedeno, z důvodů vysoké výpočetní (a tudíž i časové) složitosti je častou praktickou potřebou skládat křivky z částí. Přirozenou potřebou potom je zaručit spojité, případně hladké navazování ve spojovacích bodech. Mějme dvě racionální Bézierovy křivky P0, P1, ..., Pn,w 0, w1, ..., wn a Q0, Q1, ..., Qn, h 0, h 1, ..., h n. Křivka, která vznikne navázáním obou, bude spojitá, právě když bude bod Pn = Q0. Vzniklá křivka bude hladká, pokud bude platit: Pn = Q0 dále, w n = h0 a w n-1.(Pn - Pn-l) = h1(Q1 - Q0).
 |
|
Obr. 8.3 Kvadrika určená racionální Beziérovou křivkou |
Applet 8.3 Kvadrika určená racionální Beziérovou křivkou |
Největším přínosem. racionálních Bézierových křivek je bezesporu možnost manipulace s tvarem křivky bez změny polohy bodů řídicího polygonu.
Obrázek (Obr. 8.3) ukazuje, jak je možno pomocí racionální Beziérovy křivky vytvářet kvadriky. Bod P2 bývá označován jako shoulder point. Prostým dosazením lze ukázat, že pro wl = 0 je výsledná křivka přímkou, pro w 1 < 1 elipsou (resp. její částí), pro w 1 = 1 parabolu a konečně pro w l > 1 hyperbolou.
Obr. 12.4 ukazuje vlastnosti racionální Bézierovy kubiky.
Sledované body na křivce jsou zobrazeny kroužkem. Z uvedených obrázků je možno vyvodit, jak se zachovají sledované body při translaci řídicího bodu a také při změně váhy řídicího bodu. Vidíme také, že racionální kubika je vhodná pro tvorbu křivek, u kterých potřebujeme vytvářet prudké zlomy.
Obr. 8.4 Vlastnosti racionální Bézierovy
kubiky :
translace (vlevo) a změna váhy bodu P1 (w1
= 1, 3, 7, 10) (vpravo)
Applety 8.4 Vlastnosti racionální
Bézierovy kubiky :
translace (vlevo) a změna váhy bodu P1 (w1
= 1, 3, 7, 10) (vpravo)
Applet pro experimenty :