Neuniformní racionální B-splajn křivky (NURBS - non uniform rational B-spline) jsou dvojím zobecněním B-splajn křivek. Termín neuniformní je odvozen od vzdálenosti uzlů ve smyslu parametru t, která nemusí být u těchto křivek konstantní. Racionalita odpovídá předchozímu výkladu..
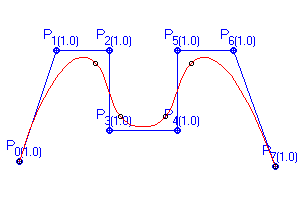
Obr. a applet 11.1 NURBS křivka stupně 3 definována pro uzlový vektor {0, 0, 0, 0, 1, 2, 3, 4, 5, 5, 5, 5}
Křivka NURBS je určena n + 1 body řídicího polynomu, uzlovým vektorem U délky m + 1 a stupněm křivky p. Uzlový vektor pro křivku NURBS procházející prvním a posledním bodem řídicího polynomu má tvar :
U = {0, 0, . . . 0, tp+1, . . . tm-p-1, b , b , . . . , b }.
Hodnoty uzlů musí být neklesající, tedy : ti+1 >= ti. Sekvence nul na začátku, stejně jako sekvence posledních hodnot (obvykle voleno b = 1) má násobnost p + 1. Zbývajících hodnot je m + 1. Mezi počtem uzlů m + 1, stupněm křivky p a počtem bodů řídicího polygonu n + 1 platí vztah :
m = n + p + 1.
( 11.2 )
Křivka NURBS je určena vztahem :
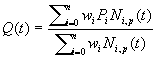 ,
,
kde wi je váha i-tého bodu řídicího polygonu a Ni,p(t) jsou normalizované B-splajn bázové funkce určené rekurentním vztahem :
![]()
![]()
( 11.4 )
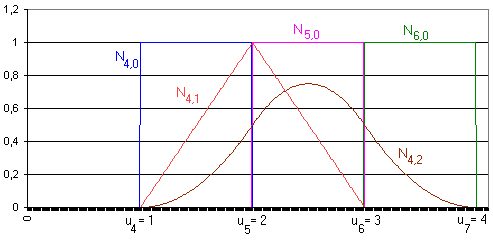
Obr. 13.2 Ukázka B-splajn bázových funkcí stupně 0...2
Jiný zápis využívá racionální B-splajn báze:
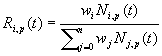
( 11.5 )
Vztah ( 11.3 ) lze pak zapsat jednodušeji :
![]()
( 11.6 )
První derivace NURBS křivky má tvar [Peig91]
![]() .
.
( 11.7 )
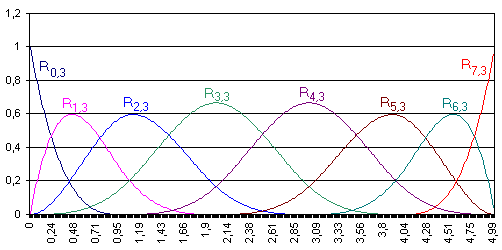
Obr. 11.3 Racionální B-splajn báze
Křivky NURBS mají tyto vlastnosti :
Zejména čtvrtá vlastnost je důležitá pro tvorbu jednotlivých datových struktur, které reprezentují jak "klasické" geometrické tvary, jako jsou např. kružnice (Obr. 11.4) či parabola, tak i volné (angl. free-form). Nevýhodou je, že reprezentace klasických objektů není jednoduchá.
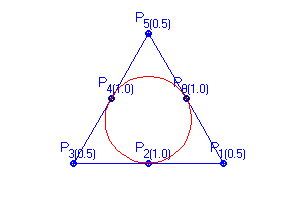
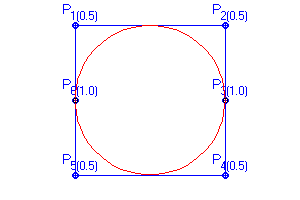
Obr. 11.4 Kružnice definovaná jako NURBS
Applety 11.4 Kružnice definovaná jako NURBS
Jak bylo uvedeno, posloupnost uzlů musí být neklesající, ale je možné, aby dva nebo více uzlů mělo stejnou hodnotu - hovoříme o násobnosti uzlů. Násobnost uzlu může zdegenerovat segmentu křivky do jediného bodu.
Vliv násobnosti bodu (zde P2) na tvar křivky je znázorněn na (Obr. 14.5). Obr. 14.6 pak ukazuje vliv stupně p na křivku.
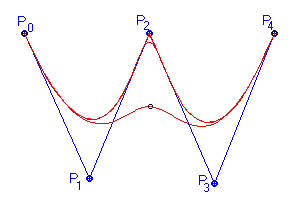
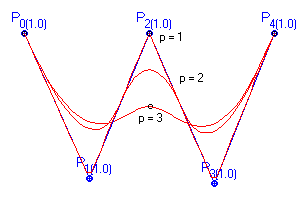
Applet 11.5 Násobnost bodu (P2) |
Applet 11.6 Vliv stupně NURBS křivky |
Applet pro experimenty :