12. Použití křivek ve 3D

Křivky, popsané v předchozích kapitolách, se díky svým vlastnostem hojně využívají ve 3D a to především při generování povrchů (je to způsobeno tím, že křivky a povrchy jsou si v jistých směrech podobné).

Tato kapitola nepopisuje detailní konstrukce 3D těles a jejich zobrazování, avšak má pouze ukázat jak lze některé z uvedených křivek využít ke konstrukci třírozměrných těles. Pro hlubší seznámení s problematikou zobrazování ve 3D tímto odkazuji čtenáře na literaturu tímto problémem se zabývající.

12.1 Operátory pro generování povrchů ze křivek

Existuje řada známých operací jako např. tažení (angl. extrusion), otáčení (angl. revolution) či vedení (angl. ruled) pro tvorbu povrchů. Pro tvorbu povrchů pomocí těchto operátorů se nejčastěji používá křivka NURBS, kterou se např. předdefinuje profil či obrys daného tělesa (2D) a z něj se pomocí operátorů vygeneruje 3D objekt.

12.1.1 Tažení

Povrchy těles, které se vytvářejí pomocí operátoru tažení jsou navrhovány tak, že se pomocí křivky nadefinuje profil (tzv. profilová křivka) a pak se pomocí operátorů tažení "táhne" tato křivka v určitém směru. Jestliže má profilová křivka tvar :

( 12.1 )

pak vzorec pro tažený povrch je :

( 12.2 )

Kde v (konstantní isoparametrická křivka) je původní profil a u (konstantní isoparametrická křivka) je úsečka definující směr tažení, zde je použita lineární NURBS křivka (t.j. R²(v)).

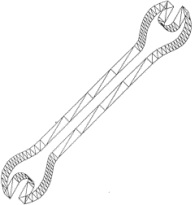
Obr.12.1 Klíč vytvořený pomocí tažení

12.1.2 Otáčení

Povrchy vytvářené pomocí otáčení jsou generovány za využití křivky (např. NURBS), která leží v xz-rovině. Povrch je vygenerován tak, že se křivka otočí o 360^O okolo osy z. Požadovaný povrch (Obr. 12.2) má tvar :

( 12.3 )

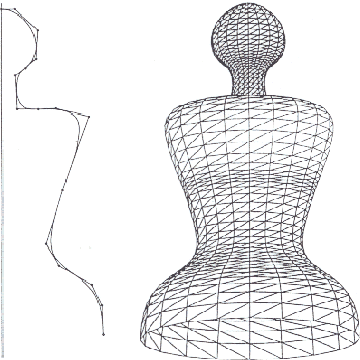
Obr. 12.2 Povrch vytvořený pomocí otáčení

Obr. 12.2 ukazuje model vytvořený pomocí otáčení profilu. Řídící síť se sestává z 9 rohových řídicích bodů a 9 středových bodů (na hranách). Dále pak každý z řídicích bodů je použit pro generování 9 řídicích bodů čtverce.

12.1.3 Vedené (řízené) povrchy (Přímkové plochy)

Povrchy vytvářené pomocí operátoru vedení (řízení) využívají toho, že každý bod, který koresponduje s daným parametrem t křivky, je propojen pomocí úsečky s jiným bodem na jiné křivce.

Takto se například vytvářejí povrchy mezi dvěmi křivkami NURBS :

1. Zvýší se stupeň křivky, která je bližší pozorovateli na stupeň křivky vzdálenější.
2. Sjednotí se uzlové vektory obou křivek.
3. Křivky se osadí novým uzlovým vektorem a sjednotí tak, aby měly stejný počet řídicích bodů.
4. Povrch se vytvoří za pomocí řídicích bodů a uzlových vektorů obou křivek. Tento postup je podobný jako postup při tvorbě povrchu operátorem tažení kdy každá křivka se stává řádkem hodnot v matici řídicích bodů.

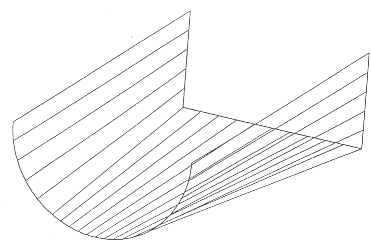
Obr. 12.3 zobrazuje vedený povrch mezi půlkružnicí a polovinou čtverce. Tento vedený povrch byl vytvořen pomocí u = konstantních isoparametrických čar (přímé čáry) rovnoměrně rozmístěných okolo čtverce a nerovnoměrně okolo kružnice.

Obr. 12.3 Vedený povrch

12.2 Plochy určené polynomy

V předchozí kapitole byla zmíněna tvorba povrchů 3D těles za využití jedné (maximálně dvou) křivek a případného operátoru. Tato kapitola se zabývá generování ploch definovaných pomocí polynomů, které se používají pro vytváření 2D křivek. Následující text potvrzuje, že pomocí 2D křivek se dají jednoduše generovat 3D plochy.

12.2.1 Interpolační plochy

Mějme dáno (m + 1)(n + 1) opěrných bodů P_i,j, dále pak (m + 1) parametrů u_i a (n + 1) parametrů v_j. Opěrnými body P_i,j lze proložit síť P(u, v), kde P(u_i, v_j) = P_i,j pro i = 0 ,. . ., m a  j = 0,. . .,n.

Nejčastěji se používají plochy určené vektorovým polynomem

( 12.4 )

musí platit :

( 12.5 )

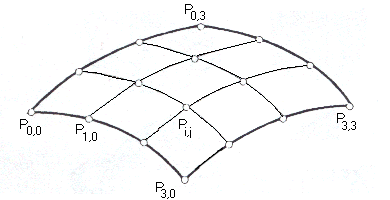
Obr. 12.4 Interpolační plocha určená 16-ti body

12.2.2 Bézierovy plochy

Bézierova plocha stupně (m, n) je definována vzorcem :

( 12.6 )

Kde P_i,j tvoří řídící síť Bézierovy plochy a B_i^m(u), B_jⁿ(v) jsou Bernsteinovy polynomy. Výraz B_i^m(u)B_jⁿ(v) tvoří Bernsteinovy polynomy dvou proměnných u,v stupně (m, n).

Pro tyto polynomy platí (podobné vlastnosti jako ve 2D) :

1. Nezáporná hodnota : B_i^m(u)B_jⁿ(v) >= 0 pro " i, j, m, n, u, v.

1. Jednotkový součet pro (u, v)  Î <0, 1>x<0, 1>

Platí-li: n = m = 3, pak Bézierovu plochu plochu nazýváme Bézierovým bikubickým plátem :

( 12.7 )

Bernsteinovy polynomy :

B₀(t) = (1 - t)³
B₁(t) = 3t(1 - t)²
B₂(t) = 3t²(1 - t)
B₃(t) = t³

( 12. 8 )

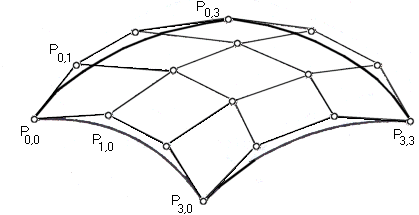
Obr. 12.5 Bézierův bikubický plát

12.2.3 De Casteljau algoritmus

Bod na Bézierově ploše lze vypočítat opakovaným použitím de Casteljau algoritmu, pak lze rovnici Bézierovy plochy zapsat ve tvaru :

( 12.9 )

kde : , j=0, . . ., n jsou Bézierovy křivky stupně n.

( 12.10 )

12.2.4 B-splajn plochy

B-splajn plocha stupně (k, 1) je určena :

( 12.11 )

Body P_i,j tvoří řídící síť B-splajn plochy N_i^k(u), N_j^l(v) jsou normalizované bázové funkce.

Parametrizace je dána uzlovými vektory :

U = (u₀ = . . . = u_k, u_k+1, . . . , u_m, u_m+1 = . . . = u_m+k+1),

V = (v₀ = . . . = v_l, v_l+1, . . . , v_n, v_n+1 = . . . = v_n+l+1), kde u, v Î <0, 1>

Vztah N_i^k(u) N_j^l(v) reprezentuje B-splajn bázové funkce dvou proměnných stupně (k, l).

Vlastnosti bázových funkcí :

1. Nezáporná hodnota : N_i^k(u) N_j^l(v) 3 0 pro všechny hodnoty : i, j, k, l, u, v.
2. Jednotkový součet : pro (u, v) Î <0, 1>x<0, 1>.
3. Lokální vlastnost : N_i^k(u) N_j^l(v) <> 0 pro (u, v) Î <u_i, u_i+k+1>x<v_j, v_j+l+1>

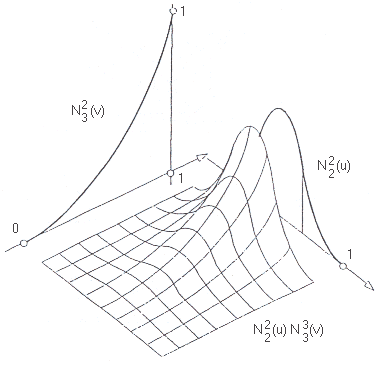
Obr. 12.6 B-splajn bázová plocha N₂²(u) N₃³(v)

Pro m = n = 3 pak B-splajn plochu nazýváme bikubickou B-spline plochu (někdy též Coonsův plát). Vzorec výpočtu tohoto plátu je určen :

( 12.12 )

a báze mají tvar :

B₀(t) = (1 - t)³/6
B₁(t) = (3t³ - 6t² + 4)/6
B₂(t) = (-3t³ + 3t² + 3t + 1)/6
B₃(t) = t³/6

( 12.13 )

NURBS

Návod na používání appletů