Roku 1964 používal J. C. Ferguson metodu pro generování křivek, která je řízena dvěma body a vektory v nich (Obr. 3.1).
|
|
Obr. 3.1 Fergusonova kubika |
Applet 3.1 Fergusonova kubika |
Krajní body jsou významné pro položení křivky (křivka jimi prochází). Vektory pak určují míru vyklenutí křivky. Čím je velikost vektoru větší, tím více se k němu křivka přimyká. Obr. 3.2 demonstruje změnu tvaru křivky, je-li první vektor konstantní a druhý vektor mění pozvolna směr o 180O.
Křivka je zadána body P0, Pl a vektory P0', P1'. Rovnice výsledné křivky
má tvar:
P(t) = P0F1(t) + P1F2(t) + P0'F3(t) + P1'F4(t),
|
|
|
| Obr. 3.2 Vliv tečného vektoru na Fergusonovu kubiku | Applet 3.2 Vliv tečného vektoru na Fergusonovu kubiku |
kde F1, F2, F3, F4 jsou kubické Hermitovské polynomy tvaru:
F1(t) = 2t3 - 3t2
+ 1,
F2(t) = -2t3 + 3t2,
F3(t) = t3 - 2t2 + t,
F4(t) = t3 - t2
a t Î <0, 1>. Položíme-li t = 0 je P(0) = P0. Analogicky pro t = 1 je P(1) = P1. Křivka tedy prochází krajními body. Zderivujeme-li P(t) podle t a dosadíme t = 0 a t = l, vyplyne, že: P'(0) = P0' a P'(1) = P1'. Tečné vektory v krajních bodech výsledné křivky jsou identické s těmi, které zadal uživatel.
Maticový zápis:
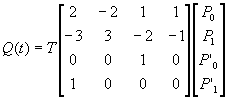
( 3.3 )
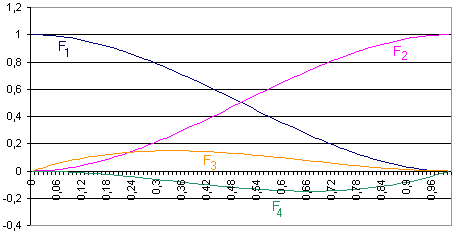
Obr. 3.3 Hermitovské polynomy
P(t) je kubikou, neboť z rovnic ( 3.1 ) a ( 3.2 ) plyne, že se jedná o součet polynomů stupně maximálně tři.
Položíme-li P0' = P1' = P1 - P0, aproximujeme touto metodou úsečku.
Spojitost při navazování oblouků je zaručena, pokud je roven poslední bod předchozího oblouku prvnímu bodu oblouku následujícího. Spojitost prvních derivací (hladkost) je zaručena identitou vektorů P1' předchozího a P0' následujícího oblouku.
Applet pro experimenty :