Interpolace pomocí Lagrangeova polynomu patří k jednomu z nejstarším pokusu vést křivku libovolným počtem bodů. Aby bylo možno polynom vypočítat, je nutno znát souřadnice n bodů, jimiž má křivka procházet a dále musí být splněna podmínka, že posloupnost interpolovaných bodů musí být uspořádané dle souřadnice x:
xi < xi+1 pro " i = 0 ..n
( 2.1 )
Interpolační polynom stupně n je potom definován vztahem:
![]()
( 2.2 )
kde polynom pi(x) se vypočítá podle vzorce:
![]() pro i = 0...n
pro i = 0...n
( 2.3 )
![]()
( 2.4 )
Výpočet hodnot interpolačního polynomu lze zjednodušit a to pomocí výpočtu řádkových součinových koeficientů Di a součinu diagonálních prvků Pn+1(x).
![]()
![]()
![]()
![]()
( 2.5 )
![]()
( .6 )
Lagrangeův polynom stupně n se nyní vypočítá:
![]()
( 2.7 )
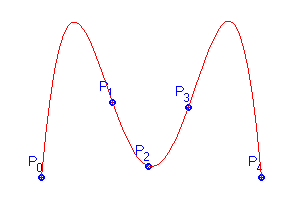
Obr. 2.1 a applet Interpolace Lagrangeovým interpolačním polynomem
Applet pro experimenty :