V letech 1959 - 62 používali P. E. Béziere a nezávisle na něm P. de Casteljau tutéž metodu návrhu aproximačních křivek. Jelikož manipulace s vektory u Fergusonových kubik je poměrně nenázorná, je Bézierova metoda podstatně populárnější. Vychází totiž pouze ze zadání řídicího polygonu bodů, který určuje tvar výsledné křivky [Bézi72].
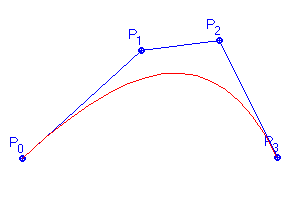
Bézierova kubika je zadána čtyřmi body P0, P1, P2 a P3. Vychází z prvního bodu P0 a končí v bodě posledním P3. Vyklenutí je řízeno body P2 a P3 (Obr. 5.1).
 |
|
Obr. 5.1 Bézierova kubika |
Applet 5.1 Bézierova kubika |
Bézierova kubika je určena vztahem:
![]()
kde t Î <0,1> a B0, B1, B2, B3 jsou kubické polynomy tvaru:
B0(t) = (1 - t)3,
B1(t) = 3t(1 - t)2,
B2(t) = 3t2(1 - t),
B3(t) = t3.
( 5.2 )
a maticový zápis:
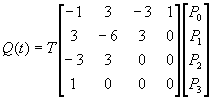
( 5.3 )
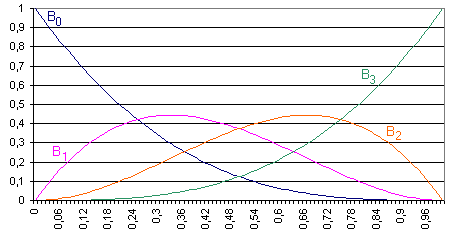
Obr. 5.2 Kubické Bernsteinovy polynomy
Položíme-li t = 0 a dosadíme do vztahu ( 5.1 ), je P(0) = P0, analogicky pro t =1 je P(1) = P3. Křivka tedy opět prochází krajními body. Zderivujme P(t) a dostaneme
![]()
( 5.4 )
Dosazením do tohoto vztahu za t = 0 a t =1 vyplyne, že:
P'(0) = 3(P0 - P1),
P'(1) = 3(P2 - P3).
( 5.5 )
Tečné vektory mají vždy směr spojnice dvojice krajních bodů a velikost mají rovnu trojnásobku vzdálenosti bodů.
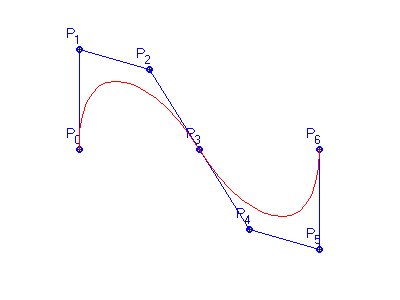
Dva Bézierovy oblouky budou spojeny hladce, bude-li zaručena jejich spojitost (tj. poslední bod předchozího oblouku je identický s prvním následujícího, nebo křivka prochází posledním a prvním bodem) a pokud budou identické tečné vektory. Z toho jednoznačně plyne, že druhý bod následující křivky je určen posledními dvěma body křivky předchozí (Obr. 5.2).
 |
|
Obr. 5.3 Hladké spojení dvou Bézierových kubik |
Applet 5.3 Hladké spojení dvou Bézierových kubik |
Applet pro experimenty :