Všichni odborníci na elektrotechniku a spoje jsou do jisté míry obeznámeni s Heavysideho diferenciální formou třetí a čtvrté Maxwellovy rovnice, totiž

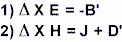
V těchto rovnicích představuje ' derivát zohledňující čas, E sílu elektrického pole, H intenzitu magnetického pole, J hustotu proudu, B hustotu magnetického toku v µH (mikro Henry) a D reprezentuje dielektrický posun = 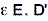rovněž nazývaný posuvný proud.
Rovnice 1) je Faradayův zákon, zatím co za rovnici 2) vděčíme Maxwellovi, který přidal k Ampérovu zákonu ono D' , což je 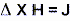udržující zachování náboje či jeho kontinuity, čímž získáme formu J + D', vyjadřující skutečnou úhrnnou hodnotu proudu.

Bohužel, v pochopení těchto rovnic mnohým ještě brání spousta potíží s pojmy, což nevyhnutelně vede k podstatným nedostatkům v uplatnění jejich významu v rámci technického využití (Myslíte, že jste v tom byli sami?). Jedním z důvodů nedostatečného vniknutí do dané problematiky je patrně neschopnost uznat skutečný fyzikální význam vektorových operací div a grad. Mnoho textů a odborných článků jejich matematické jemnosti sice často podrobně líčí, ale je jen málo popisů jejich fyzikální interpretace, shrnuté v praktických, prostých termínech.
(Autor v této souvislosti v dalším textu často používá slova "curl", čímž je myšleno něco, co se z menšího zakřivení mění v něco s větším zakřivením, asi jako spirálová kostra šnečí ulity nebo spirálovitě roztočený pramen vlasů. V podstatě lze říct, že jde o zakřivení ve smyslu Fibonacciho matematiky. p. př.)

Nadto si často neuvědomujeme, že rovnice 1) a 2) obsahují neobyčejně cenné informace, a to:
a) že časové změny magnetického pole vytvářejí buď elektrické anebo elektromagnetické pole, a co je ještě důležitější, že
b) změny toku proudu nebo časové změny elektrického pole, nebo obojího zároveň, vybudí magnetické pole.
Prosím přečtěte si to znovu a všimněte si, že k vybuzení magnetického pole nepotřebujeme proud protékající vodičem.

Esence Maxwelových rovnic, zprostředkovaná v bodech a) a b), znamená, že jde o reaktivní, neboli pole produkující rovnice.
Fyzikální a matematicko-technickou důležitost povahy buzení pole lze ještě lépe převést a pochopit, když tvary rovnic 1) a 2) obrátíme:

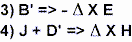
Tyto reverze vedou nejen k lepšímu porozumění obsahu Maxwellových rovnic (který v běžně užívané formě zůstává skrytý), ale i k lepšímu pochopení a uznání povahy elektromagnetizmu vyvolávaného časovými změnami, a s ním spojeným technickým využitím.

Příkladem významného technického využití, realizovatelného pouze pomocí reverzního tvaru Maxwellovy 4. rovnice, je nedávno vyvinutý revoluční systém "antény s kříženým polem" (Crossed-Field Antenna - CFA), v níž je Poyntingův vektor S přímo slučován ze samostatně stimulovaného E (elektrického) a H (magnetického) pole ( S = E X H ).
S představuje elektromagnetické záření, které obsahuje obě složky vyzařovaného pole, E a H, a X definuje vektorový součin, což znamená, že obě složky vůči sobě musí být ve správné časové relaci, fázovém úhlu a pozici. Jinými slovy, můžeme-li samostatně vytvořit obě pole a vhodně je kombinovat, nepotřebujeme ani kousek drátu, jímž by protékal proud. Podstatným rysem těchto antén je nejen malá velikost konstrukce, ale i to, že je navíc i nezávislá na vyzařované vlnové délce, což s ohledem na dosavadní teorii o anténách a jejich konstrukčním provedení představuje skutečně pozoruhodné pojetí. (Tohle si zarámujte a pověste na zeď.).

Podle líčení ve většině učebnic tkví podstata Faradayova zákona (rovnice 1) v tom, že elektrické pole může souviset s rychlostí změn magnetického pole. Také tento rys elektromagnetizmu lze vyjádřit elegantnější a informativnější cestou - reverzí rovnice 1) tak, abychom dostali tvar 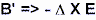 říkající, že pokud časové změny magnetického toku B' budí elektrické pole E, pak se negativní "curl" distribuovaného indukovaného E pole rovná příčině (zdroji) B'. šipka => v této souvislosti signalizuje, že zdroj na levé straně vyvolává nebo vytváří stav, platný na pravé straně. Záporné znaménko zde manifestuje Lenzův zákon. Aplikace obrácené formy Faradayova zákona je plně rozvinuta v teorii transformátoru, kde časové změny magnetického toku vytvářejí, tzn. indukují, zpětné elektromagnetické pole. Povšimněte si, že v reverzní formě Faradayova zákona je E pole indukováno z B' a nemusí nutně souviset s nezávislým elektrickým polem, vybuzeným z volného náboje podle Gaussova zákona.

Zvažme nyní rovnici 2). V magnetostatice bylo vždy akceptováno, že magnetické pole vytváří podle Ampérova zákona proud. Pro objasnění významu této výpovědi prostřednictvím smysluplnější fyzikálně-matematické podoby, by měl být Ampérův zákon vyjádřen takto: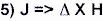
  to znamená, že J (proudová hustota) vytváří magnetické pole H, takže se "curl" H rovná zdroji J. Je také známo (a často ignorováno), že magnetické pole může souviset buď s proudem, anebo s časovými změnami elektrického pole, jak je uvedeno výše. U posledně zmíněného zdroje magnetického pole se odkazuje na Maxwellův zákon, ale totéž lze vyjádřit mnohem informativněji: 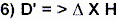  tzn., posuvný proud D' (D pole měnící se v čase) budí magnetické pole H, takže se "curl" distribuovaného H pole rovná zdroji D'. Nyní vidíme jak významná je reverze rovnice 2) do tvaru rovnice 4), tzn. J + D' => D X H, která by nyní měla být interpretována jako J + D'; obojí může vybudit magnetické pole H, takže "curl" distribuovaného H pole je rovný zdroji J + D'. Znaménko plus může, a mělo by být, interpretováno stejně jako logický symbol OR (NEBO).

Mnozí si žel neuvědomují, že H pole může kdykoli představovat kombinaci dvou samostatných polí, indukovaných nezávislými typy zdrojů, tzn., pohybem náboje a posuvným proudem.

Tato teorie nemusí být uplatněna JEN na antény...

(Výňatek z článku THE CROSSED-FIELD-ANTENNA, Part I. (A Lot of heavy Theory)
http://www.antennex.com/preview/cfa/cfa.htm
Autoři: Maurice C. Hately GM3HAT & Ted Hart W5QJR
Překlad pro WM magazín © gewo 2002, red. překladu "Hello"